When doing my last performance tests for bool packing, I got strange results sometimes. It appeared that one constant generated different results than the other. Why was that? Let’s have a quick look at branching performance.
The problem
Just to recall (first part, second part) I wanted to pack eight booleans (results of a condition) into one byte, 1 bit per condition result. The problem is relatively simple, but depending on the solution you might write code that’s 5x…8x times slower than the other version.
Let’s take a simple version that uses std::vector<bool>:
staticconstintThresholdValue= X;
std::unique_ptr<int[]> inputValues =PrepareInputValues();
std::vector<bool> outputValues;
outputValues.resize(experimentValue);
// start timer
{
for(size_t i =0; i < experimentValue;++i)
outputValues[i]= inputValues[i]>ThresholdValue;
}
// end timerAnd see the results:
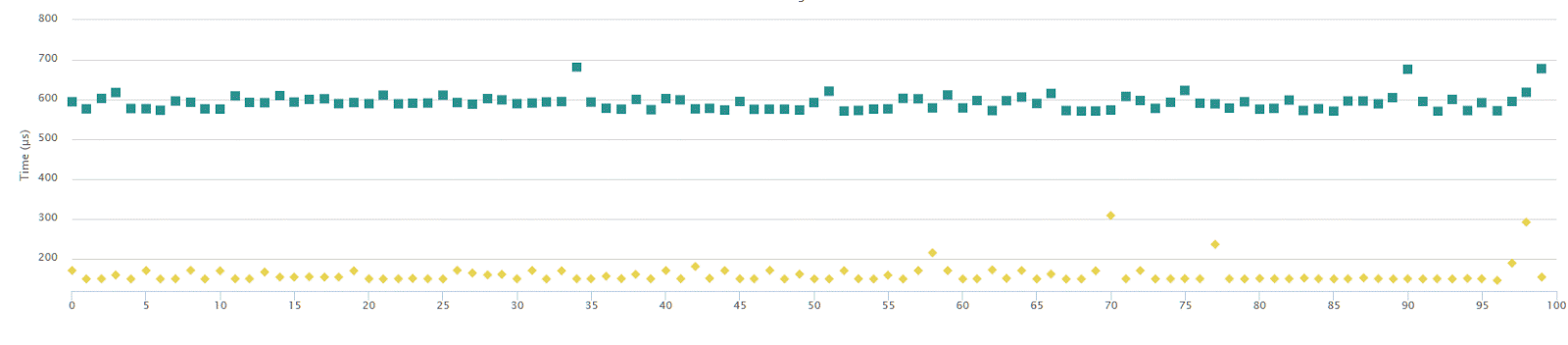
The chart shows timings for 100 samples taken from running the code, vector size (experimentValue) is 1mln.
Do you know what the difference between the above results is?
It’s only X - the value of ThresholdValue!
If it’s 254 then you got the yellow performance, if it’s 127, then you got those green, blue squares. The generated code is the same, so why we see the difference? The same code can run eve 4x slower!
So maybe vector implementation is wrong?
Let’s use a (not optimal) manual version:
uint8_tOutByte=0;
int shiftCounter =0;
for(int i =0; i < experimentValue;++i)
{
if(*pInputData >Threshold)
OutByte|=(1<< shiftCounter);
pInputData++;
shiftCounter++;
if(shiftCounter >7)
{
*pOutputByte++=OutByte;
OutByte=0;
shiftCounter =0;
}
}And the results:
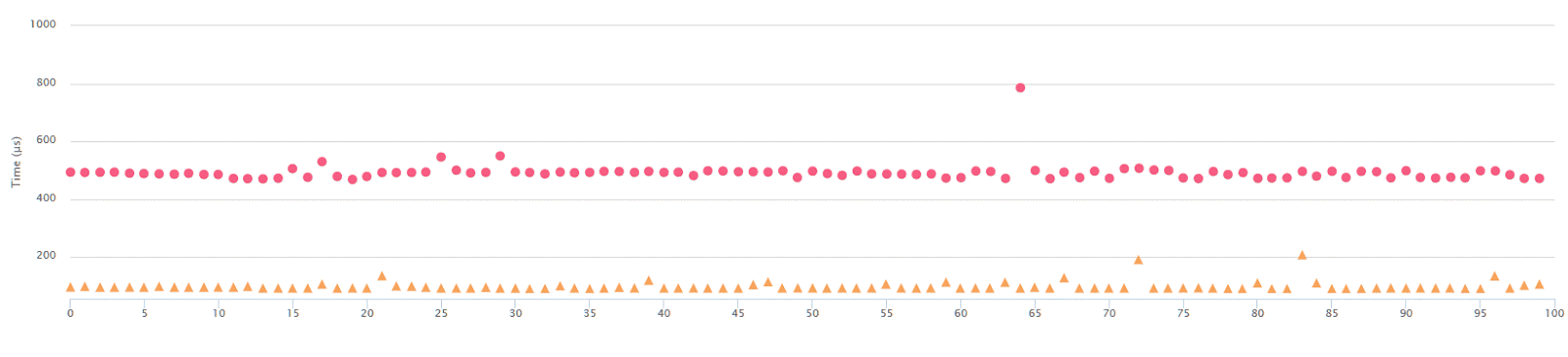
Again, when running with Threshold=127, you get the top output, while Threshold=254 returns the bottom one.
OK, but also some of the versions of the algorithm didn’t expose this problem.
For example, the optimized version. That packed 8 values at ‘once’.
uint8_tBits[8]={0};
constint64_t lenDivBy8 =(experimentValue /8)*8;
for(int64_t j =0; j < lenDivBy8; j +=8)
{
Bits[0]= pInputData[0]>Threshold?0x01:0;
Bits[1]= pInputData[1]>Threshold?0x02:0;
Bits[2]= pInputData[2]>Threshold?0x04:0;
Bits[3]= pInputData[3]>Threshold?0x08:0;
Bits[4]= pInputData[4]>Threshold?0x10:0;
Bits[5]= pInputData[5]>Threshold?0x20:0;
Bits[6]= pInputData[6]>Threshold?0x40:0;
Bits[7]= pInputData[7]>Threshold?0x80:0;
*pOutputByte++=Bits[0]|Bits[1]|Bits[2]|Bits[3]|
Bits[4]|Bits[5]|Bits[6]|Bits[7];
pInputData +=8;
}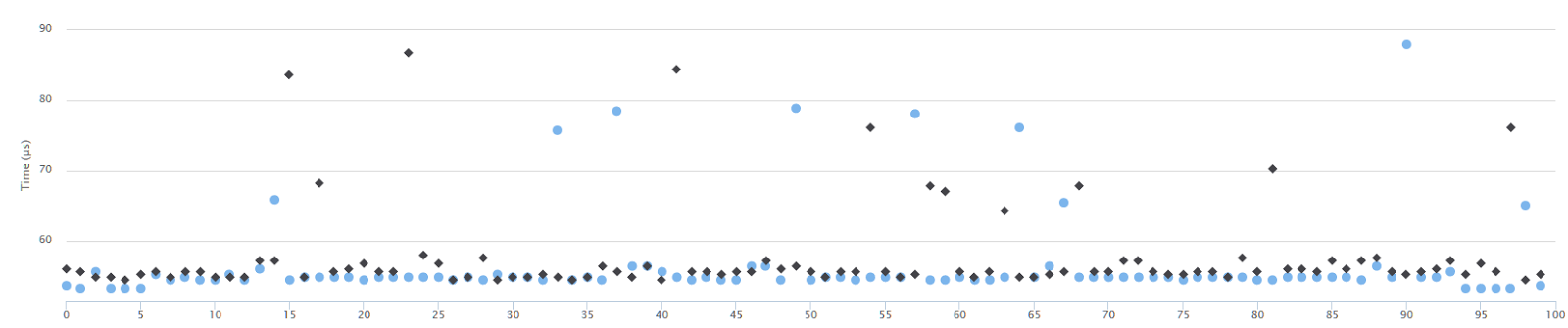
The samples are not lining up perfectly, and there are some outliers, but still, the two runs are very similar.
And also the baseline (no packing at all, just saving into bool array)
std::unique_ptr<uint8_t[]> outputValues(newuint8_t[experimentValue]);
// start timer
{
for(size_t i =0; i < experimentValue;++i)
outputValues[i]= inputValues[i]>ThresholdValue;
});
// end timer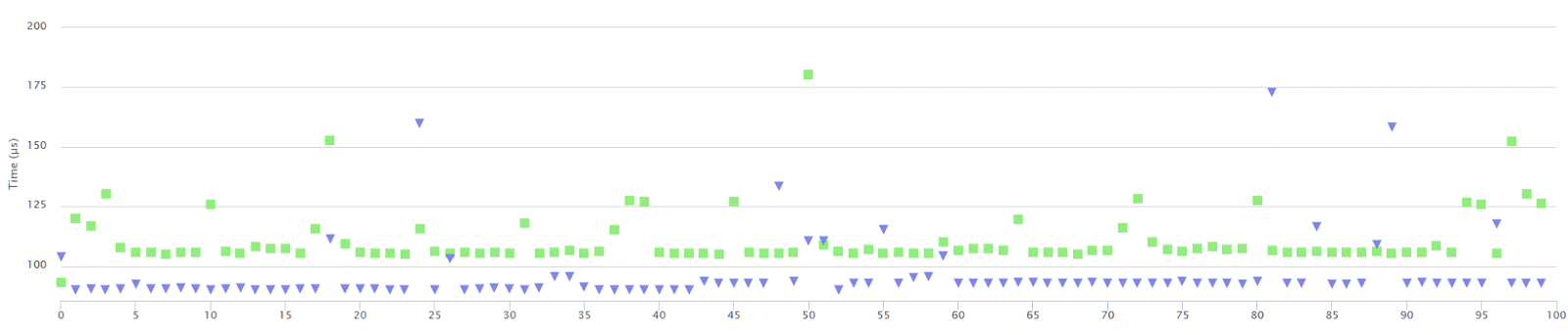
This time, Threshold=254 is slower… but still not that much, only few percents. Not 3x…4x as with the first two cases.
What’s the reason for those results?
The test data
So far I didn’t explain how my input data are even generated. Let’s unveil that.
The input values simulate greyscale values, and they are ranging from 0 up to 255. The threshold is also in the same range.
The data is generated randomly:
std::mt19937 gen(0);
std::uniform_int_distribution<> dist(0,255);
for(size_t i =0; i < experimentValue;++i)
inputValues[i]= dist(gen);Branching
As you might already discover, the problem lies in the branching (mis)predictions. When the Threshold value is large, there’s little chance input values will generate TRUE. While for Threshold = 127 we get 50% chances (still it’s a random pattern).
Here’s a great experiment that shows some problems with branching: Fast and slow if-statements: branch prediction in modern processors @igoro.com. And also Branch predictor - Wikipedia.
Plus read more in The Software Optimization Cookbook: High Performance Recipes for IA-32 Platforms, 2nd Edition
For a large threshold value, most of my code falls into FALSE cases, and thus no additional instructions are executed. CPU sees this in it’s branch history and can predict the next operations. When we have random 50% pattern, the CPU cannot choose the road effectively, so there are many mispredictions.
Unfortunately, I don’t have tools to measure those exact numbers, but for me, it’s a rather clear situation. Maybe you can measure the data? Let me know!
But why the other code - the optimized version didn’t show the effect? Why it runs similarly, no matter what the constant is?
Details
Let’s look at the generated assembly: play @ godbolt.org.
Optimized version (From MSVC)
$LL4@Foo:
cmp DWORD PTR [ecx-8],128;00000080H
lea edi, DWORD PTR [edi+1]
lea ecx, DWORD PTR [ecx+32]
setg BYTE PTR _Bits$2$[esp+8]
cmp DWORD PTR [ecx-36],128;00000080H
setle al
dec al
and al,2
cmp DWORD PTR [ecx-32],128;00000080H
mov BYTE PTR _Bits$1$[esp+8], al
setle bh
dec bh
and bh,4
cmp DWORD PTR [ecx-28],128;00000080H
setle dh
dec dh
and dh,8
cmp DWORD PTR [ecx-24],128;00000080H
setle ah
dec ah
and ah,16;00000010H
cmp DWORD PTR [ecx-20],128;00000080H
setle bl
dec bl
and bl,32;00000020H
cmp DWORD PTR [ecx-16],128;00000080H
setle al
dec al
and al,64;00000040H
cmp DWORD PTR [ecx-12],128;00000080H
setle dl
dec dl
and dl,128;00000080H
or dl, al
or dl, bl
or dl, ah
or dl, dh
or dl, bh
or dl, BYTE PTR _Bits$2$[esp+8]
or dl, BYTE PTR _Bits$1$[esp+8]
mov BYTE PTR [edi-1], dl
sub esi,1
jne $LL4@Foo
pop esi
pop ebxAnd for first manual version: https://godbolt.org/g/csLeHe
mov edi, DWORD PTR _len$[esp+4]
test edi, edi
jle SHORT $LN3@Foo
$LL4@Foo:
cmp DWORD PTR [edx],128;00000080H
jle SHORT $LN5@Foo
movzx ecx, cl
bts ecx, eax
$LN5@Foo:
inc eax
add edx,4
cmp eax,7
jle SHORT $LN2@Foo
mov BYTE PTR [esi], cl
inc esi
xor cl, cl
xor eax, eax
$LN2@Foo:
sub edi,1
jne SHORT $LL4@Foo
$LN3@Foo:
pop edi
pop esi
ret 0As we can see the optimized version doesn’t use branching. It uses setCC instruction, but this is not a real branch. Strangely GCC doesn’t use this approach and uses branches so that the code could be possibly slower.
SETcc– sets the destination register to 0 if the condition is not met and to 1 if the condition is met.
See Branch and Loop Reorganization to Prevent Mispredicts | Intel® Software
Great book about perf:Branch and Loop Reorganization to Prevent Mispredicts | Intel® Software
See also this explanation for avoiding branches: x86 Disassembly/Branches wikibooks
So, if I am correct, this is why the optimized version doesn’t show any effects of branch misprediction.
The first, non-optimal version of the code contains two jumps in the loop, so that’s why we can experience the drop in performance.
Still, bear in mind that conditional moves are not always better than branches. For example read more details at Krister Walfridsson’s blog: like The cost of conditional moves and branches.
Summary
Things to remember:
- Doing performance benchmarks is a really delicate thing.
- Look not only at the code but also on the test data used - as different distribution might give completely different results.
- Eliminate branches as it might give a huge performance boost!
Charts made with Nonius library, see more about in my micro-benchmarking library blog post.
A question to you:
- How do you reduce branches in your perf critical code?
